Here's the mathematical equation...
Posted on: October 2, 2017 at 13:45:16 CT
https://wikimedia.org/api/rest_v1/media/math/render/svg/8db00e47193ff9d4e5c0f96c9e4d2fdc01bc574a
https://en.wikipedia.org/wiki/Bertrand%27s_box_paradox
The correct answer of 2/3 can also be obtained as follows:
Originally, all six coins were equally likely to be chosen.
The chosen coin cannot be from drawer S of box GS, or from either drawer of box SS.
So it must come from the G drawer of box GS, or either drawer of box GG.
The three remaining possibilities are equally likely, so the probability that the drawer is from box GG is 2/3.
Alternatively, one can simply note that the chosen box has two coins of the same type 2/3 of the time. So, regardless of what kind of coin is in the chosen drawer, the box has two coins of that type 2/3 of the time. In other words, the problem is equivalent to asking the question "What is the probability that I will pick a box with two coins of the same color?".
Bertrand's point in constructing this example was to show that merely counting cases is not always proper. Instead, one should sum the probabilities that the cases would produce the observed result; and the two methods are equivalent only if this probability is either 1 or 0 in every case. This condition is correctly applied in the second solution method, but not in the first.
https://en.wikipedia.org/wiki/Bertrand%27s_box_paradox
The correct answer of 2/3 can also be obtained as follows:
Originally, all six coins were equally likely to be chosen.
The chosen coin cannot be from drawer S of box GS, or from either drawer of box SS.
So it must come from the G drawer of box GS, or either drawer of box GG.
The three remaining possibilities are equally likely, so the probability that the drawer is from box GG is 2/3.
Alternatively, one can simply note that the chosen box has two coins of the same type 2/3 of the time. So, regardless of what kind of coin is in the chosen drawer, the box has two coins of that type 2/3 of the time. In other words, the problem is equivalent to asking the question "What is the probability that I will pick a box with two coins of the same color?".
Bertrand's point in constructing this example was to show that merely counting cases is not always proper. Instead, one should sum the probabilities that the cases would produce the observed result; and the two methods are equivalent only if this probability is either 1 or 0 in every case. This condition is correctly applied in the second solution method, but not in the first.
Please explain why this message is being reported.
MESSAGE THREAD
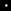 Here's the mathematical equation... - JeffB MU
Here's the mathematical equation... - JeffB MU


